Aperiodic Monotiles: A Revolutionary Tool for Analyzing Complex Systems
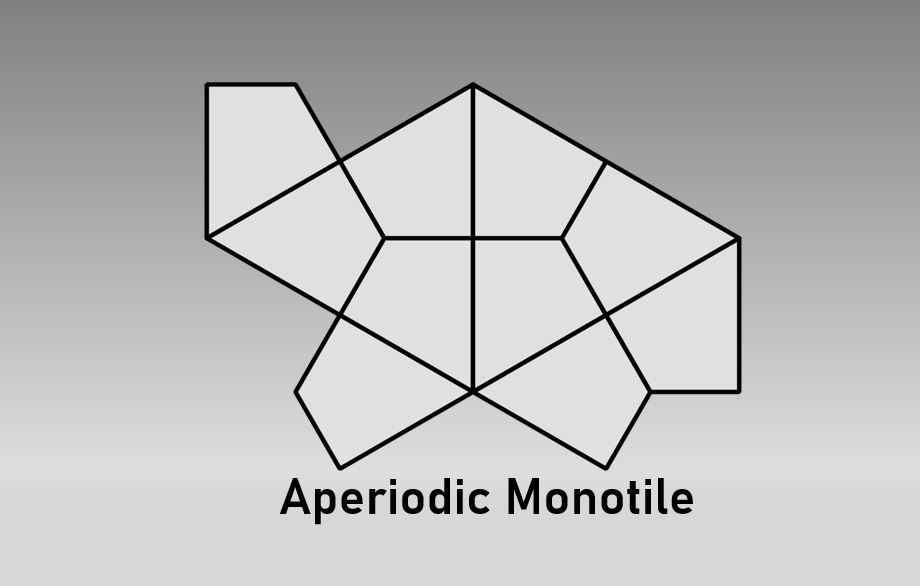
Aperiodic tiling, often referred to as aperiodic monotiles or an “Einstein”, are a fascinating branch of mathematics that has been attracting a great deal of interest from physicists, materials scientists, and mathematicians. Aperiodic monotiles are simple patterns or tiles that have no visible periodicity and can be used to tile the plane. In contrast to ordinary tiling’s, which feature a repeating pattern, this indicates that the pattern created by the tiles never repeats.
When Robert Berger discovered the first known example of an aperiodic tile in the 1960s, he originally proposed the idea of aperiodic monotiles. However, interest in aperiodic monotiles did not really take off until the 1970s, with the discovery of the Penrose tiles.
Penrose Tiles
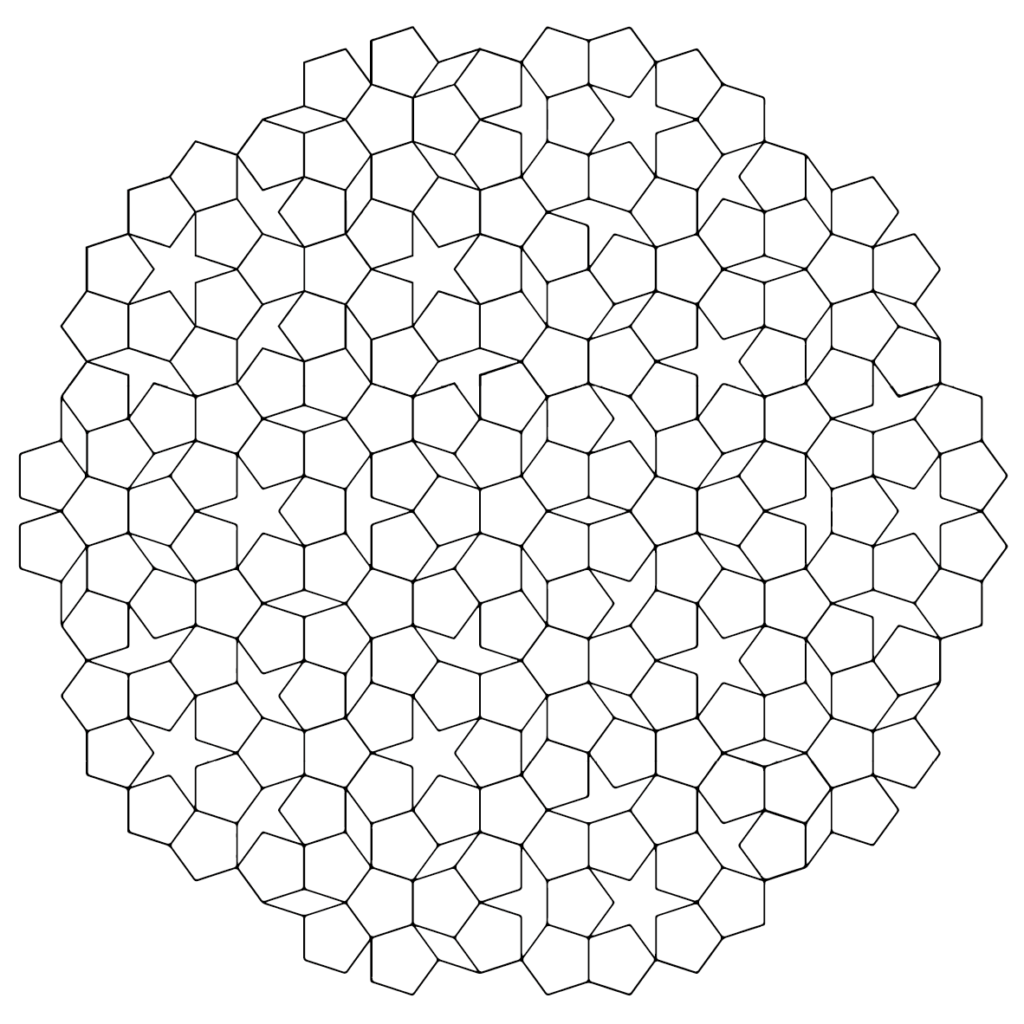
Roger Penrose, a British mathematician, discovered the Penrose tiles, which are a well-known example of aperiodic monotiles. The Penrose tiles are composed of two distinct shapes that are referred to as the “kite” and “dart” respectively. These shapes can be used in several ways to create a unique tiling pattern.
Numerous additional aperiodic monotiles have been found since the discovery of the Penrose tiles. These include tiles that are composed of three or more different forms as well as tiles that are based on more intricate mathematical structures rather than geometric shapes and are not composed of any shapes at all.
The study of aperiodic quasicrystals is one recent field of research in aperiodic monotiles. Materials with a structure that is organized but not periodic are known as quasicrystals. This indicates that the arrangement of atoms or molecules in the substance is regular, yet the arrangement does not repeat itself like a crystal lattice does. Penrose tiles are frequently used as models for aperiodic quasicrystals because of their similar behavior and regular but nonperiodic design.
Aperiodic quasicrystals have special mechanical, electrical, and optical characteristics that make them suitable in a variety of use, which has attracted the interest of researchers. For instance, it has been shown that quasicrystals are effective thermal insulators and have been employed in coatings to increase the efficiency of solar cells.
The study of aperiodic monotiles’ symmetries is one more recent area of research in this field. Aperiodic monotiles frequently display intricate symmetries that are absent from regular tilings. In contrast to regular tilings, some aperiodic monotiles, for instance, have five-fold rotational symmetry. Researchers may be able to better understand the behavior of aperiodic monotiles by understanding these symmetries, which may also have implications for the study of other complex systems.
Use of Aperiodic Monotile In Complex Mathematical Problem
Aperiodic monotiles, commonly referred to as non-periodic tiling units, are geometric forms that can be utilized to make patterns that never exactly repeat. Many mathematical issues, even some of the most challenging ones, have shown to benefit from the use of these shapes.
Aperiodic monotiles offer a framework for examining the structure of complex systems, which is one of the key ways they can be helpful in solving complex mathematical issues. For example, Aperiodic monotiles can be used to simulate the structure of quasicrystals and a variety of complex biological formations, like the branching patterns of blood arteries and trees.
Aperiodic monotiles can also be used to investigate the behavior of dynamical systems, including chaotic and self-organizing systems. Researchers can better understand the behavior of these systems and generate new techniques for forecasting it by looking at the patterns that can be produced using aperiodic monotiles.



