The Power of Trigonometry in Solving Mathematical Complex Problems
Trigonometry is the study of the relationships between triangle sides and angles. It offers a collection of powerful techniques that may be applied to a variety of mathematical issues, many of which are regarded as complex. In this article, we will look at how trigonometry can help you solve mathematically complex problems.
Relationships between Sides and Angles of Triangles
Triangles’ sides and angles can be related to one another using trigonometry. These relationships can be utilized to identify unknown triangle sides or angles in problems involving triangles. The length of a side or the size of an angle in a right triangle, for instance, can be determined using the sine, cosine, and tangent functions.
Trigonometric Identities
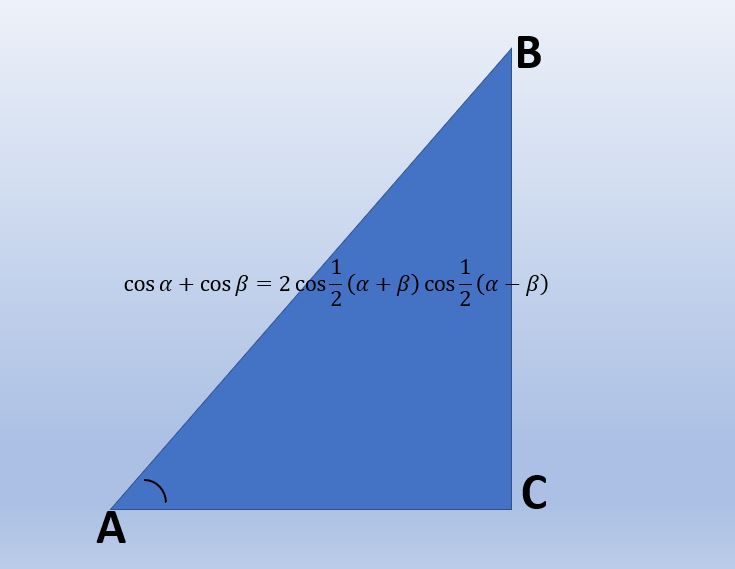
Trigonometric identities are mathematical equations that connect the relationships between the trigonometric functions. These identities can be used to prove mathematical theorems and simplify difficult trigonometric formulas. For instance, the Pythagorean identity (sin^2(x) + cos^2(x) = 1) is a fundamental identity that is utilized in a variety of trigonometry-related applications.
Calculus and Trigonometry
Trigonometry is a fundamental tool in calculus, particularly in the study of functions that involve oscillations and periodicity. The derivatives and integrals of trigonometric functions are used in a wide range of applications, including physics, engineering, and economics. Calculus is a branch of mathematics that deals with the study of rates of change and the accumulation of quantities.
Applications in Physics and Engineering
In physics and engineering, trigonometry is frequently used to address challenging mathematical issues. It can be used to calculate heights and distances, analyze forces and motion, calculate electric and magnetic fields, and analyze waves and oscillations, among other things. These applications rely on the calculus of trigonometric functions as well as the fundamental triangle relationships between sides and angles.
Uses of Trigonometry in Science
Trigonometry has numerous scientific applications in physics, astronomy, engineering, and many other disciplines. Below , we’ll discuss some uses of trigonometry in Science
1. Calculating Distance and Height
To determine the distance and height of objects that are challenging to measure directly, trigonometry is frequently used. For instance, astronomers use trigonometry to determine the distances between stars and galaxies by calculating the angles between various spots in the sky. To calculate the height of towering buildings or structures like bridges and towers, engineers also employ trigonometry.
2. Analyzing Waves and Oscillations
In order to analyze waves and oscillations, trigonometry is also used. For instance, trigonometric functions like sine and cosine are employed in physics to describe the motion of waves in many areas, such as sound and light. Trigonometry is a tool that engineers use to examine machine and building vibrations.
3. Calculating Angles and Directions
In several scientific domains, trigonometry is required to calculate angles and directions. For instance, geographers use trigonometry to determine the direction and separation between two points on a map. Trigonometry is another tool that surveyors use to calculate the angles and separations between various places on the ground.
4. Analyzing Forces and Motion
In physics and engineering, trigonometry is used to analyze forces and motion. To calculate the forces operating on a structure like a bridge or building, engineers use trigonometry. Trigonometry is a tool used in physics to determine the speed and acceleration of moving objects.
5. Calculating Electric and Magnetic Fields
Physics calculations of the electric and magnetic fields also involve trigonometry. For instance, trigonometric functions like sine and cosine constitute the foundation of equations that describe the behavior of electric and magnetic forces. Trigonometry is a tool that engineers and physicists use to determine the strength and direction of these fields in a variety of contexts.



